监督学习

一、监督学习的第一性原理

1. 本质定义

监督学习的本质问题是：

在给定输入—输出样本对 $(x, y)$ 的条件下，在某个假设空间 $H$ 中，寻找一个函数 $f$，使其在未知数据上的期望风险最小。

形式化表达：

$$\min_{f \in H} ; \mathbb{E}_{(x,y) \sim D}[L(f(x), y)]$$

这一定义揭示了监督学习的三大不变量：

维度含义
假设空间 $H$模型对世界的简化方式
损失函数 $L$对“错误”的价值判断
泛化能力对未知世界的适应能力

所有监督学习算法，本质上只是对这三者的不同取舍组合。

2. 监督学习的基本问题类型

这不是算法差异，而是输出空间结构的差异。

二、监督学习的核心认知框架

1. 假设空间视角（核心升维）

监督学习算法的根本差异，不在于公式细节，而在于：

它们假设世界“长什么样”

假设空间类型核心思想代表模型
线性假设世界可被线性关系近似线性回归、逻辑回归、GLM
距离假设相似样本有相似输出KNN
树结构假设世界可由规则切分决策树、随机森林、GBDT
最大间隔假设最安全的边界最可靠SVM
概率判别假设输出是条件概率Softmax、Logistic
时间依赖假设当前依赖历史AR / ARMA / ARIMA

2. 学习原则（跨模型不变量）

所有模型都遵循以下原则：

三、线性世界观：线性模型家族

1. 线性回归：可解释性的极致

核心假设：

输出是输入特征的线性加权组合

$$f(\mathbf{x}) = \mathbf{w}^T \mathbf{x} + b$$

学习目标：最小化平方误差

$$J(w,b) = \frac{1}{2m}\sum_{i=1}^m (f(x^{(i)}) - y^{(i)})^2$$

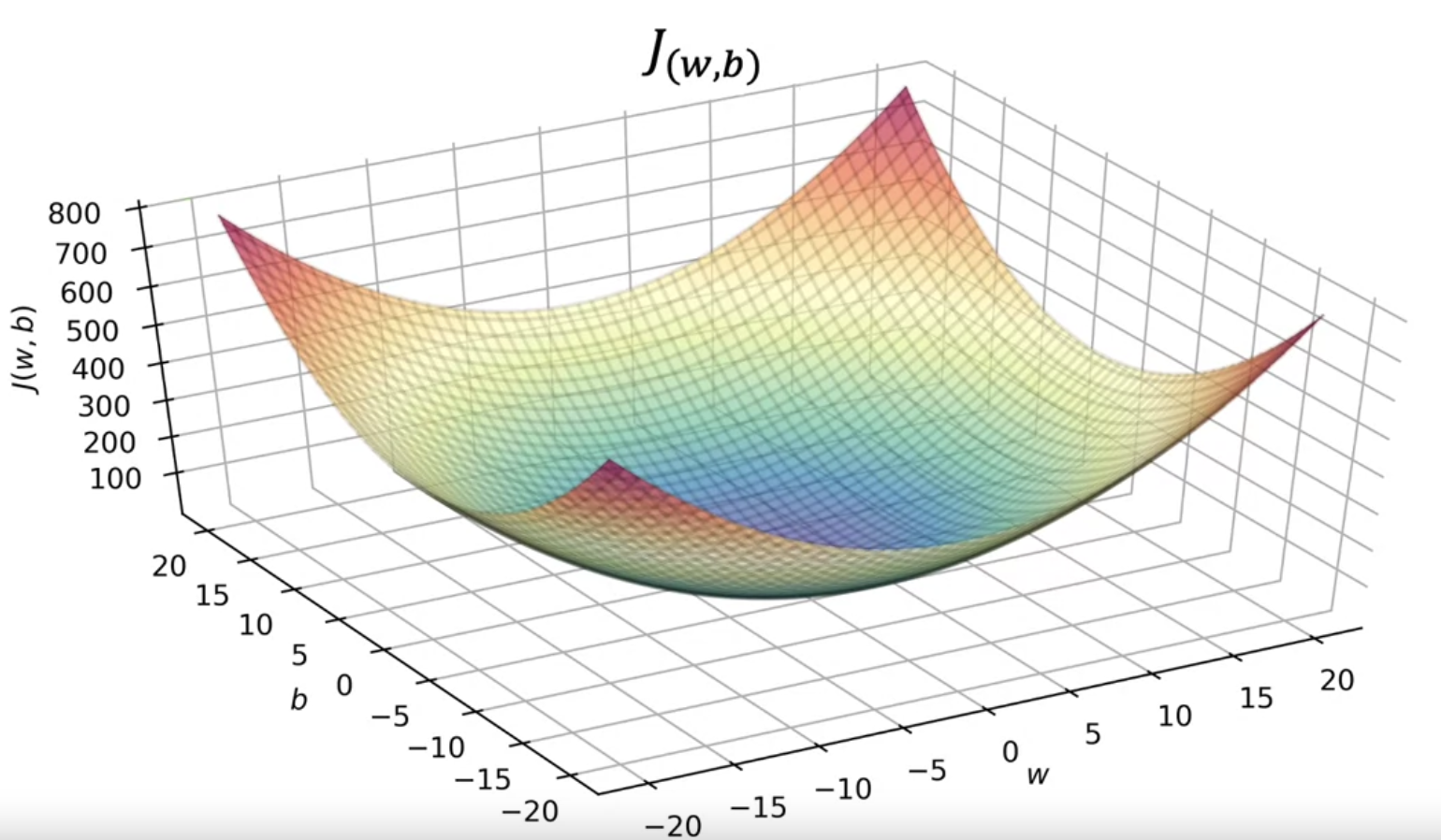
w b 不同取值对应的平面

哲学含义：

2. 多项式回归：线性形式下的非线性表达

本质不是“更复杂模型”，而是：

通过特征映射扩展假设空间

线性模型 + 非线性特征 = 表达能力提升

3. 广义线性模型（GLM）

核心突破：

统一形式：

$$y = g^{-1}(\mathbf{w}^T\mathbf{x} + b)$$

GLM 是 Logistic、Poisson 回归的理论母体。

4. 广义可加模型（GAM）

思想升级：

保留可解释性，引入受控非线性

$$y_i = \beta_0 + f_1(x_{i1}) + \cdots + f_p(x_{ip})$$

是“线性理性”向“复杂现实”的一次温和妥协。

四、概率判别世界观

1. 逻辑回归：概率化的线性分类

通过 Sigmoid 将线性输出映射为概率：

$$f(\mathbf{x}) = \frac{1}{1+e^{-(\mathbf{w}^T\mathbf{x}+b)}}$$

决策边界由 $\mathbf{w}^T\mathbf{x}+b=0$ 定义。

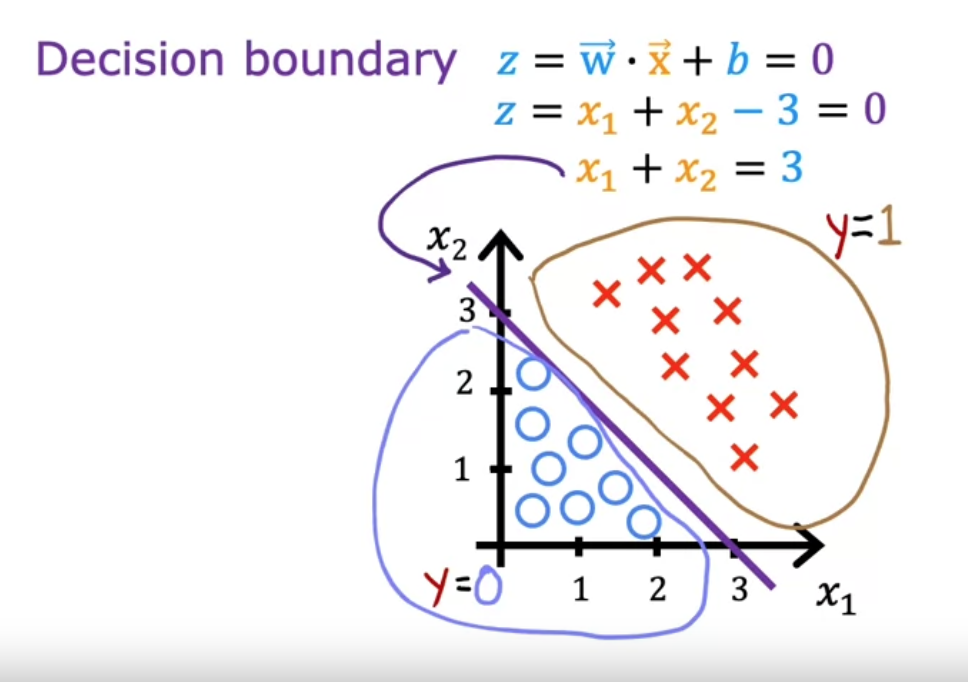
线性决策边界非线性决策边界

损失函数来源：最大似然估计（交叉熵）

2. Softmax 回归：多分类的自然推广

输出的是条件概率分布：

$$P(y=k|\mathbf{x}) = \frac{e^{z_k}}{\sum_i e^{z_i}}$$

Softmax 揭示了：

分类不是“判断”，而是“概率分配”。

五、最大间隔世界观：支持向量机

1. SVM 的核心思想

在所有可分边界中，选择最安全的那一条

即：最大化分类间隔。

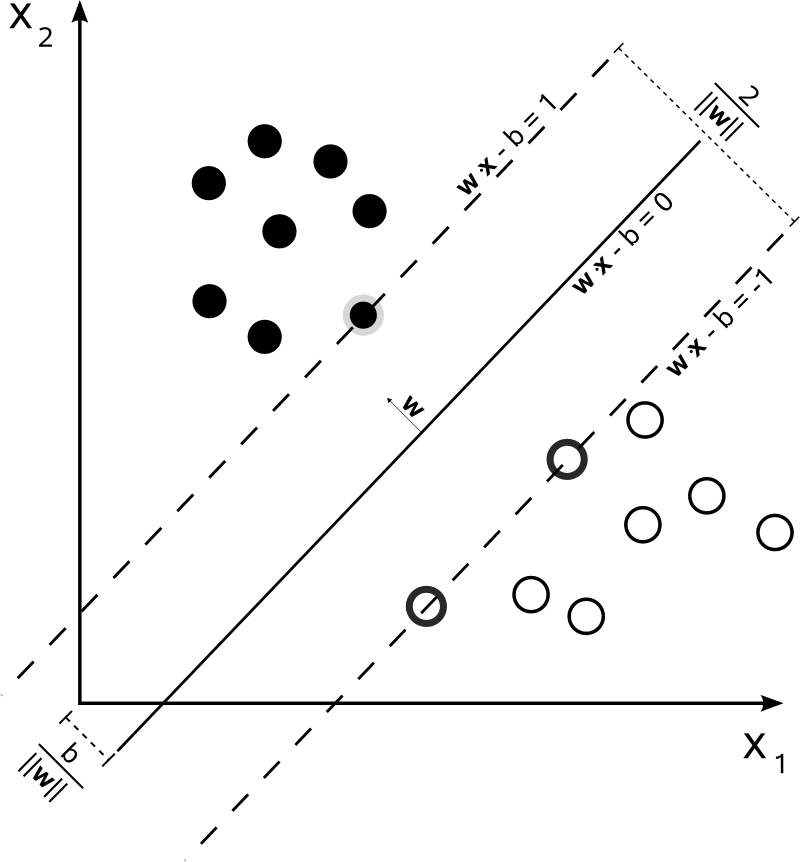
SVM的几何意义

2. 核技巧：隐式特征映射

$$k(\mathbf{x}, \mathbf{x}') = \phi(\mathbf{x})^T \phi(\mathbf{x}')$$

本质：

这是计算理性对表达能力的折中。

六、规则切分世界观：树模型家族

1. 决策树的本质

用一组 if-else 规则逼近真实函数

决策树结构示意

核心问题：

2. 不纯度度量

指标本质
熵不确定性
信息增益不确定性减少
基尼系数随机不一致概率

3. 决策树算法谱系

熵 → ID3熵 / 属性熵 → C4.5基尼 / 二叉划分 → CART

4. 剪枝：结构风险控制

本质目标一致：

用更简单的树，换取更强的泛化能力

七、集成思想：从单模型到系统理性

1. 随机森林：去相关化的并行集成

哲学本质：

多个“有偏但不相关”的模型胜过一个完美模型

2. 极端随机森林

进一步牺牲单棵树质量，换取整体多样性。

3. 梯度提升树（GBDT）

串行纠错：每一棵树都在修正过去的错误

这是函数空间上的梯度下降。

八、距离世界观：KNN

核心假设：

世界是连续的，相近即相似

权衡核心：

九、时间依赖世界观

时间序列模型的特殊性

模型核心思想
AR历史值决定现在
MA历史噪声影响现在
ARMA二者结合
ARIMA差分平稳化

十、监督学习的演进与选型方法论

1. 模型演进路径

线性模型 → 决策树 → 随机森林 → GBDT → 深度学习（预留）

2. 模型选择的四个核心约束

关联内容（自动生成）